Energetics

import numpy as np; import matplotlib.pyplot as plt
import EOBRun_module 

pars = {
    # System parametes, assuming aligned spins        
    'M'                  : 1,      # Total mass
    'q'                  : 2,      # Mass ratio m1/m2 > 1
    'chi1'               : 0.,     # Z component of chi_1
    'chi2'               : 0.,     # Z component of chi_2
    'LambdaAl2'          : 0.,     # Quadrupolar tidal parameter of body 1 (A)
    'LambdaBl2'          : 0.,     # Quadrupolar tidal parameter of body 2 (B)
    'ecc'                : 0.3,     # Eccentricity. Default = 0.
    'ecc_freq'           : 2,      # Use periastron (0), average (1) or apastron (2) frequency for initial condition computation. Default = 1

    # Initial conditions and output time grid
    'domain'             : 0,      # Time domain. EOBSPA is not available for eccentric waveforms!
    'srate_interp'       : 4096.,  # srate at which to interpolate. Default = 4096.
    'use_geometric_units': "yes",   # output quantities in geometric units. Default = 1
    'initial_frequency'  : 0.003,     # in Hz if use_geometric_units = 0, else in geometric units
    'interp_uniform_grid': "yes",  # interpolate mode by mode on a uniform grid. Default = 0 (no interpolation)

    # Modes
    'use_mode_lm'        : [1],    # List of modes to use/output through EOBRunPy

    # Output parameters (Python)
    'arg_out'            : "yes",  # Output hlm/hflm. Default = 0
}

t, hp, hc, hlm, dyn = EOB.EOBRunPy(pars)
pks = find_peaks(dyn['MOmega'], distance=150) [0]
nu  = pars['q']/(1 + pars['q'])**2
Eb = (dyn['E'] - 1.)/nu

# Plot
fig, ax = plt.subplots()
ax.plot(dyn['Pphi'], Eb)
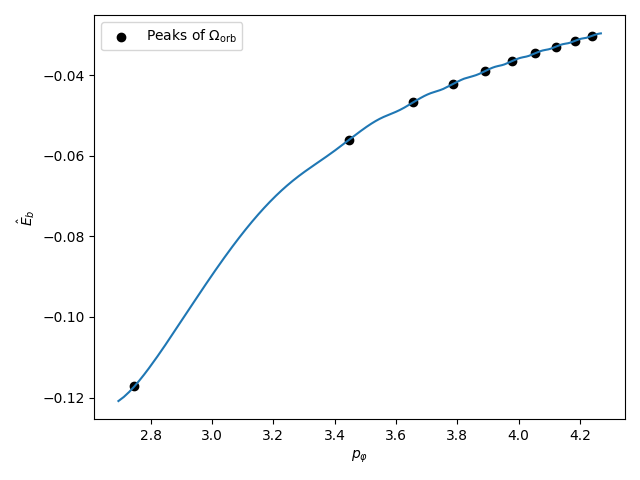
ax.scatter(dyn['Pphi'][pks], Eb[pks], color='k', label=r'Peaks of $\Omega_{\rm orb}$')

ax.set_xlabel(r'$p_\varphi$')
ax.set_ylabel(r'$\hat{E}_b$')
plt.legend()
plt.tight_layout()
plt.savefig('../template/assets/images/eobej.png')
plt.show()